Happiness Is
Happiness is
having a sister.
Sharing a sandwich.
Getting along.
Happiness is singing together when day is through,
And happiness is those who sing with you.
Happiness is morning and evening,
Daytime and nighttime too.
For happiness is anyone and anything at all
That’s loved by you.
According to Mr.
Micawber, happiness is income greater than expenditures.
Is income an absolute? If income can be negative then income is relative, NOT an absolute.
Can there be negative income? If you ask an accountant, then everything is either
a credit or a debit. The sum of credits
over a period of time is your income.
The sum of debits over a period of time are your expenses. The sum of your credits at any point in time are
your assets. The sum of your debits at
any point in time are your liabilities.
The difference between your assets and your liabilities is your net
worth. If your net worth is positive, then you
are said to be wealthy. If your net worth is negative then you are said to be in debt and possibly bankrupt.
On these definitions alone, because credits and debits are
aways positive, it would seem reasonable that income should always be positive. However there are loans which are treated
like income but are actually debits. And you can
pay for debits with previous assets, such that your change in net worth in a period
is negative. So while income may always be positive,
mathematically it is convenient to treat it as if it can also be negative.
So why does this matter?
If you act like income must always be positive you might treat it as an absolute. In this case, the distribution of income should
follow an exponential distribution which has an absolute value at zero. If instead, income can be negative, then the distribution
of income should follow a hyperbolic tangent.
The Cumulative Distribution Function for an exponential distribution is 1-e-λ*x,
but this should really be 1 - e-λ*(x-µ),
where µ is equal to zero. By contrast
the formula for a hyperbolic tangent is tanh((x-µ)*b), where in
this case b is a function of the variance, σ2.
The value µ is not only
the translation along the income axis, but also a parameter defining a random distribution
of an individual in a group.
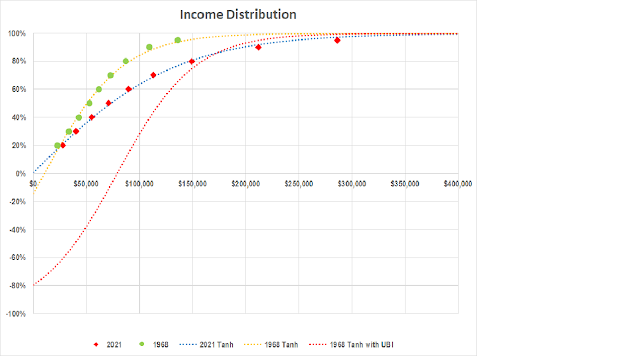
The US Census reports on the distribution of incomes. Using the distribution of incomes, adjusted for
inflation, the limit of the decile percentage, and the top 5% are shown as reported in the figure below. Both an exponential distribution and a hyperbolic tangent
fit the distribution of income very well.
However if you treat the amount of public investment at 0% as not confined
to zero, but you keep the same variance from 1968, then you end up with a completely
different distribution of income. I am calling
this amount Universal Basic Income, UBI, but this income does not have to be in cash. It can also be in the form of public education,
public healthcare, public childcare, public housing, etc. that are available to any one with little or no income.
Fitting an exponential distribution in 1968 implies a basic public expenditure of $12,327 dollar per household, while fitting to a hyperbolic tangent implies a basic public expenditure of $6,480 per household. However in 2021, the exponential distribution implies a basic public expenditure of $14,770, while the hyperbolic tangent implies a basic public expenditure of minus $1,298 per household. The fit to the exponential distribution was achieved by allowing the value of µ to be as close to zero as possible but allowing the variance to more than double. ( Ironically, mathematically the square root of the variance is called the standard deviation. Those in favor of the 2021 existing distribution of income, which requires an INCREASE in variance, also want a DECREASE in deviation). If there is no change in the variance from 1968, then the basic public expenditures, Universal Basic Income, µ, might be $58,937. At this amount, the distribution of income is almost equal for those in the top 80% . The mean income increases for those households under 80% and the mean income decreases for those over 80%. This UBI sounds like a lot, but the economy and the number of households have both increased from 1968. If the tax revenues average 20% of household income (the median, NOT the mean) then that amount is only 0.345% of the increase in tax revenues.
That the distribution of incomes does not follow an exponential distribution is apparent from the difference between the mean and median incomes. Under a true exponential distribution, the mean would be equal to the median. That it is not, and in fact the gap between the mean and the median is growing, shows that income is not an absolute and should NOT be distributed according to an exponential distribution.
The slope
of a hyperbolic tangent is the hyperbolic secant squared. In 1968 and 2021, the slope of a hyperbolic
tangent looked very much like an exponential distribution, but that does not
mean that income is an absolute. As a group it should follow a random distribution. A way to increase the distribution of
the group is to maintain the variance while increasing the “income” at zero percent.