Laffer Curve

                                                       

Everybody’s Got A Laughing Place

Everybody's got a laughin' place,
A laughin' place, to go ho-ho!
Take a frown, turn it upside-down
And you'll find yours I know ho-ho!

But nobody needs a Laffer Curve!

The Laffer Curve attempts to explain the revenue from an income tax with the rate of that income tax. It does so by assuming that this curve can be explained by a parabola. IMHO that is why there is a problem. It assumes that the sweet spot, maximum, is where the first derivative of the parabola is zero. IMHO, the curve should NOT be a single parabola but instead should be two intersecting hyperbolas. That is why there is a problem. A parabola requires that for incomes below a zero tax rate, the tax revenue be negative, and the income be imaginary, and at tax rates more than 100% the revenue be negative, and the income be imaginary.  A hyperbola approaches zero revenue, but never becomes zero or negative, and thus the  income never becomes imaginary.

A single parabola can look like two intersecting hyperbolas, but these looks can be deceiving. This behavior is better explained as the lower portion of two intersecting hyperbolas. These hyperbolas are in fact inverses of each other and the point of intersection is also defined. The tax rate should be 16.7% (1/6) of total income. This is the median tax rate, NOT the highest tax rate. If the median is 16.7%, and the lowest effective tax rate is 0%, then the highest tax rate in a normal distribution should be 33.4%. This is the effective rate, not the marginal rate. The effective tax rate is like speed; the marginal tax rate is like acceleration. They are NOT the same and should not be confused with each other. The marginal rate in tax tables depends on the number of equal tax brackets. The marginal tax rate is the percentage of the maximum tax rate which applies.  The effective tax rate is the marginal rate multiplied by that maximum rate. The tax rates should change from the lowest effective rate of 0% to the highest effective tax rate of 33.4% and the lowest income in the highest bracket should be close to the normal  maximum income. If the median household income is $74,580, in 2022 US dollars as reported by the US Census, then the normal maximum income should be twice that, $149,160 in 2023 USD income. According to the U.S. Census Bureau, the mean household income in the United States in 2022 was $105,555. If income was normally distributed, and the median is 50% then the maximum should be twice the median in a normal distribution . To still be normal if skewed, the highest income should not exceed $233,063, 2/ln(2) or ~π Times the Median Income.. The mean income should ideally be half of the highest income. The highest income tax bracket for married filing jointly in the 2023‑24 IRS tax code begins at  $693,750 and there are 7 brackets. The tax brackets using this, as well as the other highest incomes, and the 7 tax brackets are shown in the table below.

The tax brackets are only a linear approximation of what is a non-linear function.  The Census mean income occurs in the 3rd of the 7 brackets in the current IRS tables, but these tables have unequal income brackets. If the income brackets are equalized, but the highest Tax Code income is retained, then the Census mean income occurs in the 2^nd of the 7 brackets . If the highest income is π times the Census median income, then the Census mean income occurs as it should in the 4^th, middle, of the 7 income brackets.

This sounds counter-intuitive, but it is mathematically consistent. Most of the tax revenue comes from the lowest tax brackets. This is because while the rate per taxpayer is low, there are many more taxpayers in these brackets, so that the total revenue from these brackets is very high. The fixation on the rates paid by the few taxpayers in the highest brackets instead of the revenue from the majority of taxpayers in the lowest brackets has been distorting public policy. 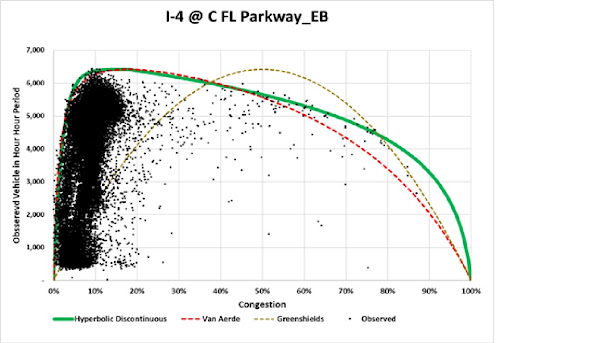By confusing marginal (second derivative) and effective (first derivative) tax rates, by having unequal tax brackets, and by using the Laffer Curve, this is inconsistent with other observations, for example observations of traffic in Florida. Those observations of traffic also suggest that the majority of observations occur before the highest volume. Those observations do NOT support a regular ( such as the one proposed by Greenshields) or irregular (highly sewed such as the one proposed by Van Aerde) parabola, but instead intersecting hyperbolas where the intersection  occurs at 1/6^th of the variance, range of congestion ( similar to tax rates in the Laffer Curve.)

Those who don’t learn from history are doomed to repeat it. Those who don’t know math are doomed to be conned.

References

Greenshields, B. (1935). A study of traffic capacity. Highway Research Record, (pp. 448-477). Washington, DC.

Van Aerde, M. (1995). A single regime speed-flow-density relationship for freeways and arterials. Washington D. C.,: Presented at the 74th TRB Annual Meeting,.